もう１０年以上前の出来事です。「１２人のグループから２人がいなくなると、残りは何人になりますか」という問題に対して、ある小学５年生は、１２÷２＝６人と解答し、それが不正解だと知ると次は１２×２＝２４人と解答しました。それでも不正解なら１２＋２＝１４人と、次から次に計算方法を変えますが、問題文を読んで内容を理解しようとはしませんでした。当時小５だったその子のこの状況を改善するのに、実に１２ヵ月かかりました。

小学校の授業で初めて「割り算」を学習するときは、どの文章問題も割り算で答えを出す問題ばかりです。それに気付いた子の一部は、「先生の難しくて退屈な説明を聞かなくても、要するに文章中に出てくる大きい方の数字を小さい方の数字で割れば答えが出るんやろ」という結論に達し、「内容を理解する」作業をやめてしまう子が出てくるのでしょう。そんな子には「答えを出す」という目的が達成できれば、もはや理屈や理由はどうでもよくなってしまいます。

そんな子にとって算数の文章問題とは「とりあえず適当に計算してみて正解したらラッキー。不正解なら次は別の計算を試していけばいずれ正解する」というものになってしまっています。だから「難しい理屈や理由はいいから何算すればいいのかだけ教えて」と、やり方だけを求めるようになってしまいます。そして小学生の間にそのような癖が染みついてしまうと、中学生になってもそうそう簡単には直すことはできなくなります。

中１の１月にコンパスによる作図を学習します。

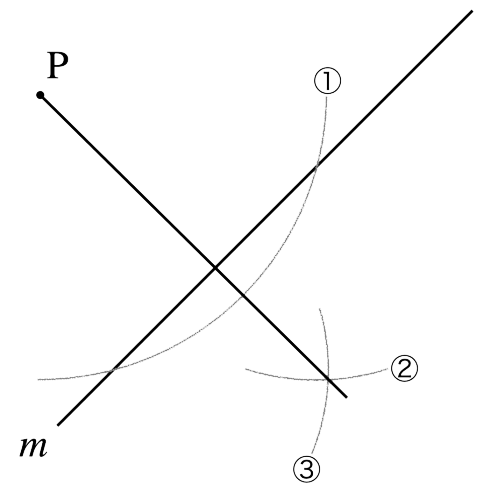
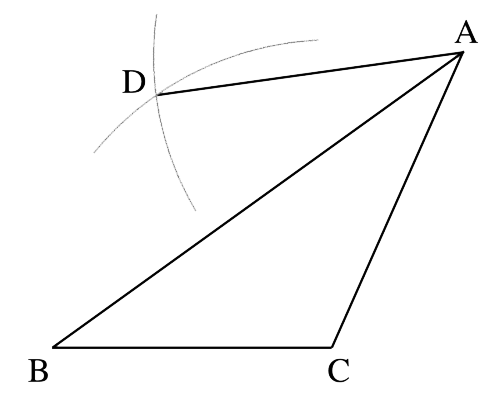
例えば下の図で「点Pを通る、直線ｍの垂線（直角に交わる直線）を作図しなさい」という問題を扱います。

この場合、下の図のように

はじめに点Pにコンパスの針を当てて①の線を引いたあと、その線と直線mの２つの交点に針を当てて②, ③の線を引き、その交点と点Pを直線でつなぐとそれが直線mの垂線になります。

が、「どうやれば解けるのか（正解となるのか）」にしか興味がない子は、そもそも今「直線mに対する垂線を引こうとしている」ということすらも認識しないまま（それが分かっていなくても、やり方さえ分かればとりあえず目の前の問題には正解できると思うのでしょう）「まず点Ｐにコンパスの針を当てて・・・」と指示通りに目的の線を引いて「できた」と満足します。ただ、それは手順を説明したとおりにこなしただけで、決して「理解した」訳ではありません。そして上の問題の図の向きが90度逆になろうとも、点Ｐが直線ｍ上にあろうとも、同じ手順で答えが出せるので「マスターした」と思うのでしょうが、このあとの練習問題はこう変化します。

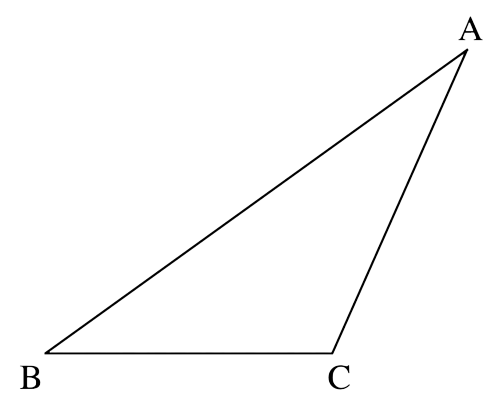
「△ABCの辺BCを底辺としたときの高さを示す線分ADを作図しなさい」

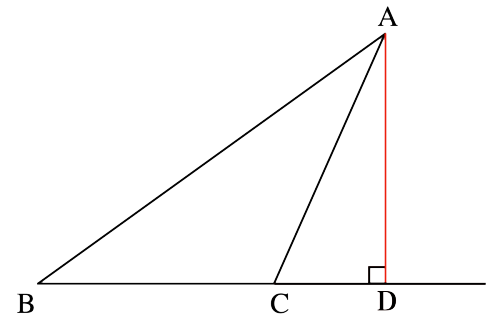
もちろん、この場合書かなければいけないのは（辺BCを底辺としたときの）三角形の高さなので、下図の赤い線であり

つまり辺BCの延長線に対して点Aから引いた垂線がこの三角形の「高さ」になるので、その前にさんざん練習したように、下の図のような「点Aを通る、直線BCの垂線」を引かなければなりません。

その前の問題はどんなに向きが変わってもすらすら作図できていたのに、この問題を目にしたとたん「分からーん。激ムズー」と言う子は、なぜそうなってしまうのか。

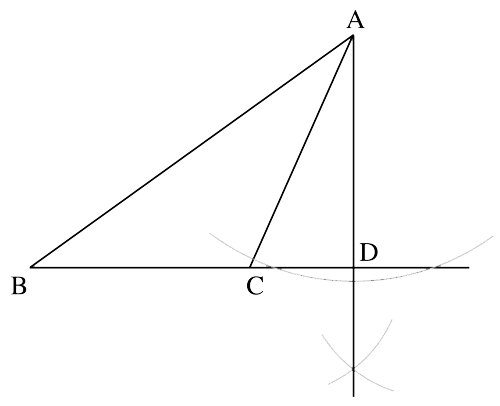
まずそもそもその前の練習の段階で「自分が一体何を書いているのか」を認識せず、ただ単純に「図を書く問題」としか捉えてなかったのだということ。だからこの問題に対しても同様に「三角形の高さにあたる線を書け」と言われているのにもかかわらず、問題文を読まないから「何を書くよう問われているのか」が分からないまま、結局下のような図を書いてしまいます。

「目の前に点と線があればまず点にコンパスの針を当てて、次に・・・・・・」と、やり方をマスターしただけですから、ちょっと問題が変われば「さっきまでの問題と違うから解けない」となるのは当然です。

そうなると何となく「とりあえずここに針を当ててこんな曲線を２本書いて交わったとこと結んでみよう」と、理屈ではなく記憶にのみ頼って、上のような図を書いてしまうのです。

こういう子は、おそらく小学３～５年の時点から「理由や理屈はどうでもいいから、やり方だけ教えて」という考えになってしまっているものと思われます。理由の説明を聞くのが面倒で退屈なので「で、結局どうすればいいと？」とやり方だけ聞いてその場をしのぐ繰り返しをしてきているのだと。 

それがはっきりと分かる事例があります。

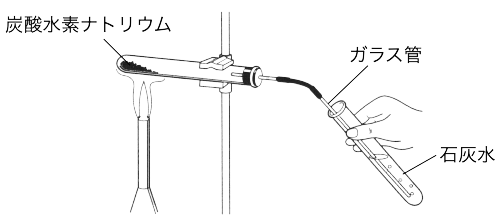
中２理科「炭酸水素ナトリウムの熱分解の実験」でよく出題される２つの問題があります。

①「火を消す前にガラス管を石灰水から抜かなければならない理由を答えなさい」

火を消して試験管の加熱をやめたら中の気体の温度は下がり始めます。気体は温度が上がるとふくらみ、温度が下がるとしぼみます。気体がしぼむと石灰水が吸い上げられてガラス管を通って加熱していた試験管に向かって逆流してしまいます。したがって答えは「石灰水が逆流するのを防ぐため」です。

②「加熱する試験管の口の方を少し下に傾けておかなければならない理由を答えなさい」

炭酸水素ナトリウムを加熱すると水が発生します。加熱している部分は熱いので水は水蒸気として発生します。が試験管の口の方は加熱部ほど熱くないため水蒸気は水になり水滴が試験管の内部につき始めます。もしもこの試験管を逆に傾けていたら、その水が加熱している方へ流れていき、高温のガラスが水で急に冷やされると試験管が割れる恐れがあります。したがって答えは「発生した水が加熱部へ流れ試験管が割れるのを防ぐため」です。

もちろん実際の授業ではこの文章を読むだけのような説明ではなく「風船だってドライヤーで中の空気を暖めたら膨らむとよ」とか「自分で家でやってみい。ガラスのコップを箸でつまんでガスコンロで加熱して、アッチアチになったあとすぐに水につけたら、コップ割れるけん。ただ親には怒られるやろうけど」とか、実際に頭に浮かぶような事例を交えながら説明します。

 ただ、「難しそうな理屈を聞いて理解するよりも暗記する方が手っ取り早い」と思う子は、「つまりこう聞かれたらこう答えればいいんやろ」と理由も何も分からずにただ暗記をするだけだから、①の質問に②の解答を答えたり、そもそも文章の内容さえも分からずにただ言葉の並びを暗記しているだけなので「加熱部が流れて逆流しないように」と訳の分からない解答を書いたりします。

例えるならその子は「赤と言われたら紫と言え」「白と言われたら茶色と言え」「青と言われたら黄色と言え」・・・これを何十個も暗記しているようなものです。それだと覚えるのも大変ですし、もしも頑張って覚えてその日のテストはなんとか乗り切っても、時間が経ったら忘れるに決まってます。だって質問と答えに何の関連もなく法則もないのですから。

 一昔前は福岡県の高校入試でも、意味は分からなくても「やり方」さえ覚えれば正解できるパターン化された問題も出題されていましたが、２０１８年に撤廃されました。それ以降は「これまでに学習してきた内容と与えられた条件をもとに自分で考える作業」を必要とする問題が増えています。

だから私は授業中はとにかく「なぜそうするのか」「○○だから××するんだよ」と常に理由を説明して聞かせ、時に「なんでと思う？」「どうすればいいか考えてみ」と考えさせながら、時おり分かってるかどうか不安な子には、「ここまで意味分かる？ 本当に？ じゃあ××するときは何で△△せないかんと？」と確認しながら授業を進めるようにしています。